|
研探新知
|
[合作探究]
师 在对一般形式推导之前,我们先思考一个特殊的简单情形:1+q+q2+…+qn=?
师 这个式子更突出表现了等比数列的特征,请同学们注意观察.
生 观察、独立思考、合作交流、自主探究.
师 若将上式左边的每一项乘以公比q,就出现了什么样的结果呢?
生 q+q2+…+qn+q n+1.
生 每一项就成了它后面相邻的一项.
师 对上面的问题的解决有什么帮助吗?
师 生共同探索:
如果记Sn=1+q+q2+…+qn,
那么qSn=q+q2+…+qn+q n+1.
要想得到Sn,只要将两式相减,就立即有(1-q)Sn=1-qn.
师 提问学生如何处理,适时提醒学生注意q的取值.
生 如果q≠1,则有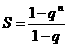 . .
师 当然,我们还要考虑一下如果q=1问题是什么样的结果.
生 如果q=1,那么Sn=n.
师 上面我们先思考了一个特殊的简单情形,那么,对于等比数列的一般情形
我们怎样思考?
课件展示:
a1+a2+a3+…+an=?
[教师精讲]
师 在上面的特殊简单情形解决过程中,蕴含着一个特殊而且重要的处理问题
的方法,那就是“错位相减,消除差别”的方法.我们将这种方法简称为“错位
相减法”.
师 在解决等比数列的一般情形时,我们还可以使用“错位相减法”.
如果记Sn=a1+a2+a3+…+an,
那么qSn=a1q+a2q+a3q+…+anq,
要想得到Sn,只要将两式相减,就立即有(1-q)Sn=a1-anq.
师 再次提醒学生注意q的取值.
如果q≠1,则有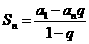 . .
师 上述过程如果我们略加变化一下,还可以得到如下的过程:
如果记Sn=a1+a1q+a1q2+…+a1q n-1,
那么qSn=a1q+a1q2+…+a1qn-1+a1qn,
要想得到Sn,只要将两式相减,就立即有(1-q)Sn=a1-a1qn.
如果q≠1,则有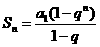 . .
师 上述推导过程,只是形式上的不同,其本质没有什么差别,都是用的“错位
相减法”.
形式上,前一个出现的是等比数列的五个基本量:a1,q,an,Sn,n中a1,q,an,Sn
四个;后者出现的是a1,q,Sn,n四个,这将为我们今后运用公式求等比数列的
前n项的和提供了选择的余地.
值得重视的是:上述结论都是在“如果q≠1”的前提下得到的.言下之意,就是
只有当等比数列的公比q≠1时,我们才能用上述公式.
师 现在请同学们想一想,对于等比数列的一般情形,如果q=1问题是什么样的
结果呢?
生 独立思考、合作交流.
生 如果q=1,Sn=na1.
师 完全正确.
如果q=1,那么Sn=nan.正确吗?怎么解释?
生 正确.q=1时,等比数列的各项相等,它的前n项的和等于它的任一项的n倍.
师 对了,这就是认清了问题的本质.
师 等比数列的前n项和公式的推导还有其他的方法,下面我们一起再来探讨一下:
[合作探究]
思路一:根据等比数列的定义,我们有: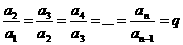 , ,
再由合比定理,则得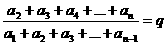 , ,
即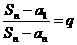 , ,
从而就有(1-q)Sn=a1-anq.
(以下从略)
思路二:由Sn=a1+a2+a3+…+an得
Sn=a1+a1q+a2q+…+a n-1q=a1+q(a1+a2+…+a n-1)=a1+q(Sn-an),
从而得(1-q)Sn=a1-anq.
(以下从略)
师 探究中我们们应该发现,Sn-S n-1=an是一个非常有用的关系,应该引起大家
足够的重视.在这个关系式中,n的取值应该满足什么条件?
生 n>1.
师 对的,请同学们今后多多关注这个关系式:Sn-S n-1=an,n>1.
师 综合上面的探究过程,我们得出:
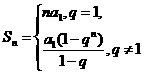 或者 或者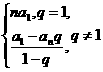
|
|
质疑答辩,排难解惑,发展思维
|
【例题1】 求下列等比数列的前8项的和:
(1)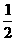 , ,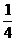 , , ,…; ,…;
(2)a1=27,a9=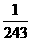 ,q<0. ,q<0.
【例题2】 某商场今年销售计算机5 000台,如果平均每年的销售量比上一年的销售量增加10%,那么从今年起,大约几年可使总销售量达到30 000台(结果保留到个位)?
|
|